Isochronal weather routing solvers are designed to do one thing: find the fastest path between two points, through a weather system, which satisfies the constraints the user has specified.
The constraints that a WR solver is able to accept and work with varies from product to product. Constraints can be thought of as a way for you to describe the routes you are interested in seeing.
Are you interested in seeing routes which sail hard into the wind to get to a destination, or would you rather sail more comfortably off the wind and arrive a little later? Do you want to avoid wind speeds that are too strong? Alternatively, do you want to avoid areas where the wind falls below some minimum speed? Do you want to only sail or are you interested in routes where the vessel is allowed to motor when things slow down?
These are all examples of constraints. Dials, or settings, that you can adjust in order to describe to the system what you are interested in seeing.
Position constraints
The LuckGrib WR solver is unique among isochronal solvers in that it can accept a series of constraint points, each of which must be left to port or left to starboard. These constraint sequences are a flexible way for you to describe the shapes of the routes you would like to see.
There are a couple of WR systems available which provide the ability for their WR solvers to navigate to a series of points, point A to point B, point B to point C, and so on. This is only useful when you are required to pass through or close by each of those points.
I believe there are no other isochrone weather routing solvers which can accomplish this generalized point constraint problem.
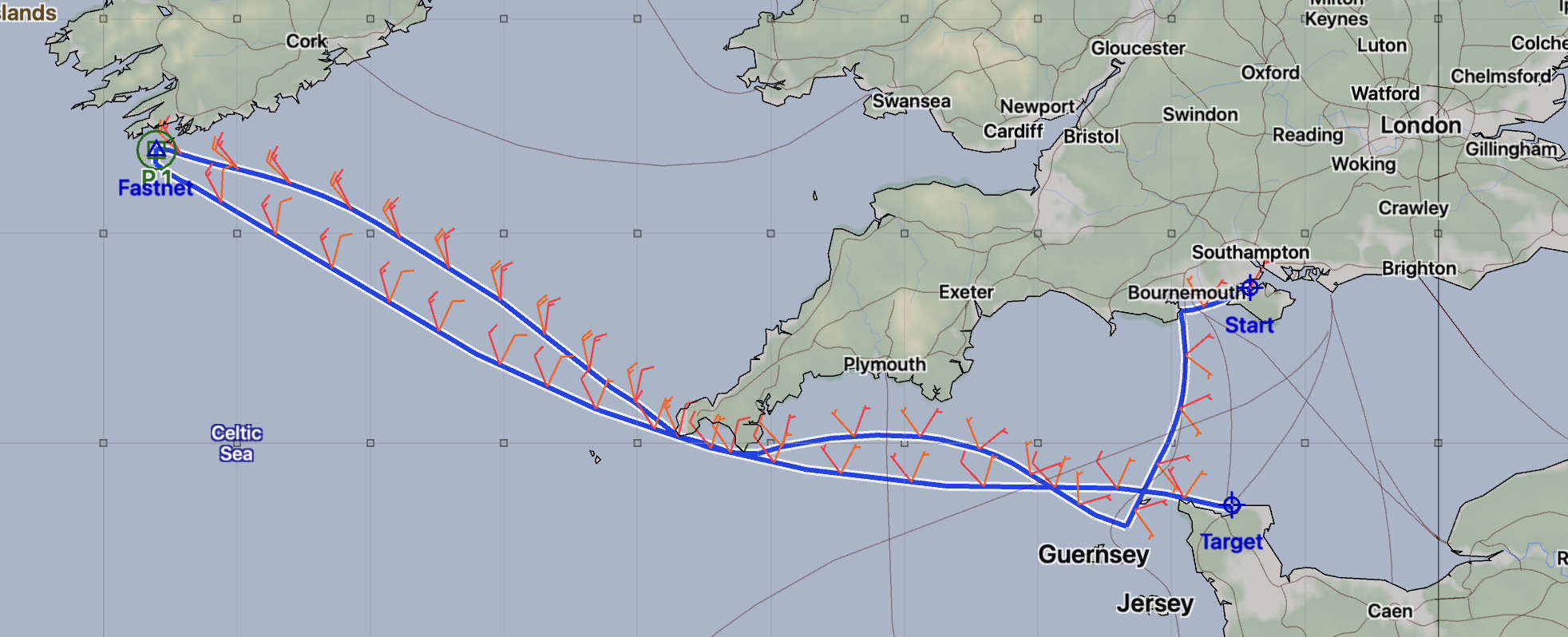
The route above is for the Fastnet race. It starts just north of the Isle of Wight, rounds the Fastnet rock and finishes at Cherbourg. This route was described to the system using a start and target point, along with a single constraint point, where the Fastnet rock is left to port.
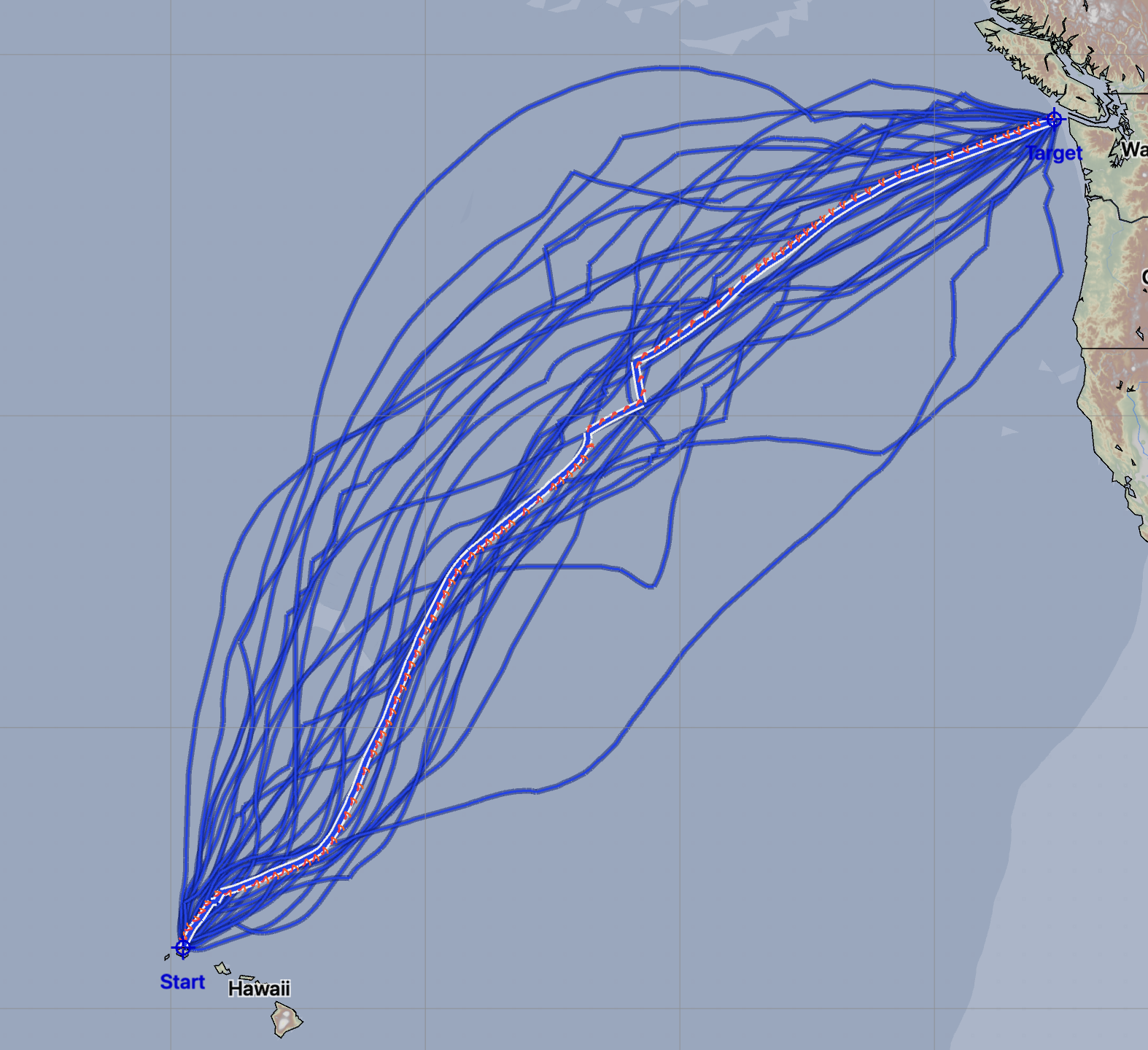
In this second example, a fast boat is shown sailing from Hawaii to Neah Bay, in March, using GEFS full wind ensemble forecast data. The routes above are unconstrained. (Note that the departue time of these routes is in March, which is a poor time for a departure for this route.)
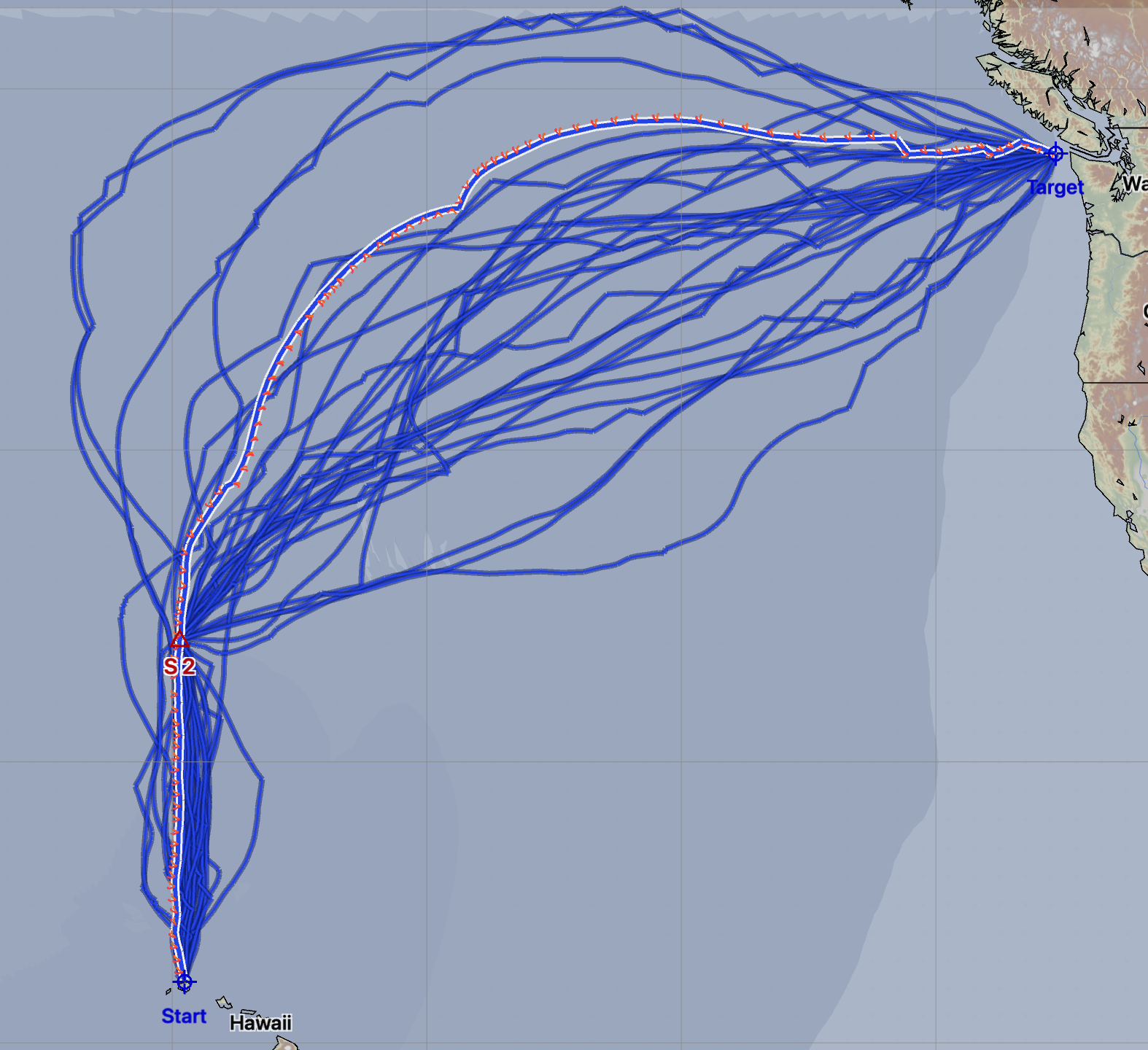
The routes above now have a single constraint point, the point labelled S2 above, which the solver must leave to starboard. Note that some of the routes pass very closely to the point and others leave the point quite far to their starboard side. These solutions are not the same as traveling to the intermediate point and then to the final point. The system is finding optimum solutions where this point is left to starboard.
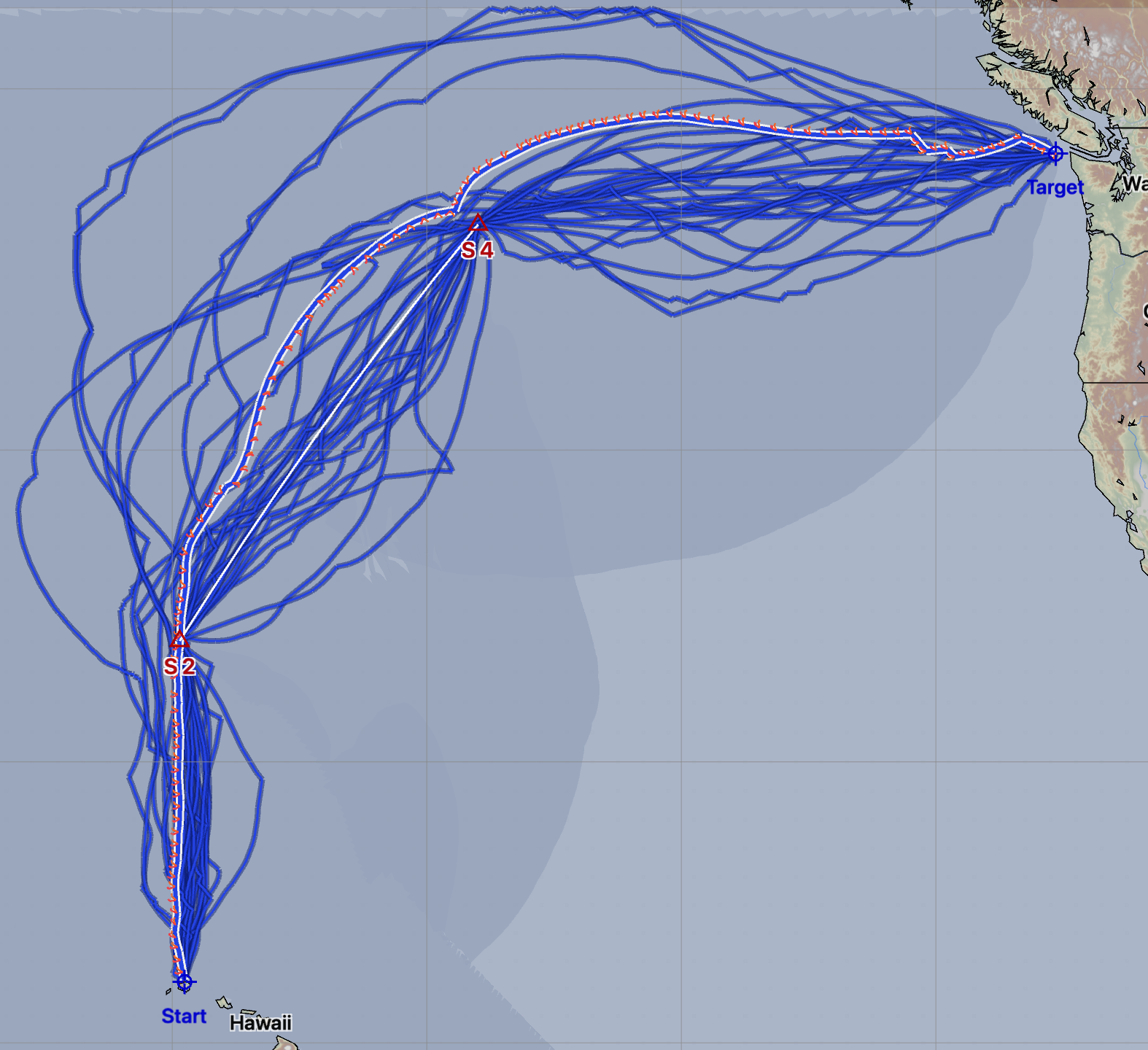
In this last example, a second constraint point has been added, which is again left to starboard. Note that some routes pass very closely to this second point and others leave it far away. The system is finding optimized routes which meet the constraints, not routes which pass through these points.
Constraints are discussed in more detail later.
Boundary constraints
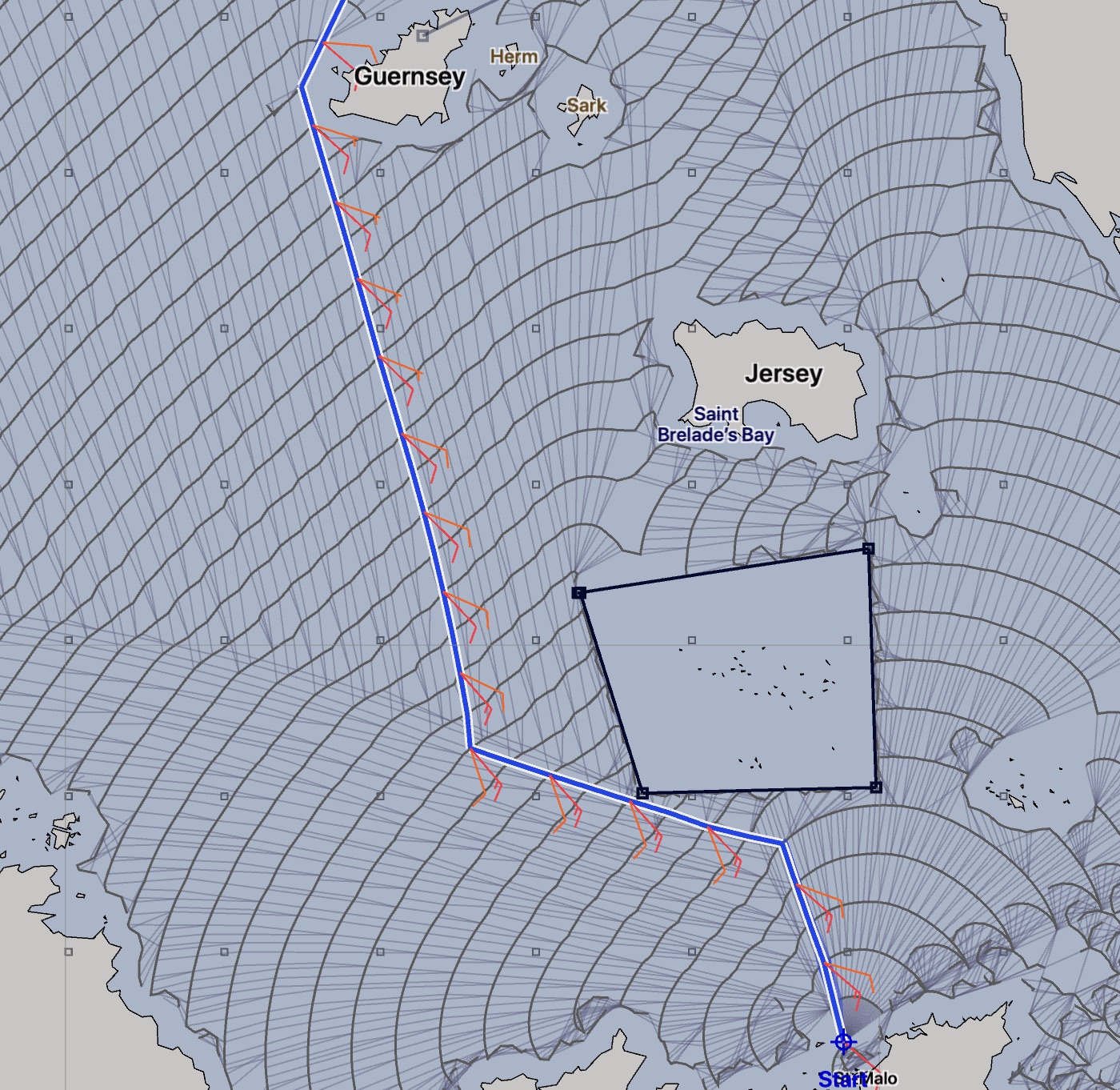
The LuckGrib WR solve is able to accept boundaries, which define lines which the WR solver must not cross. This can be used to define areas where there are known hazards (land, shallows or otherwise.) Boundaries are discussed in more detail in a section of the getting started guide.